What is a WAVEFORM??
Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.
In electronics sense its basically the representation of variation of current or voltage or power with respect to time.
Why should I study about WAVEFORMS and analyse them??
They are the easiest form of representation of time varying signals and one can immediately make out the characteristics by just looking at the waveform.
How do we classify WAVEFORMS??
Method I:
Based on direction of propagation and alternation:
- 1. Uni-directional Waveforms: These waveforms are always positive or negative in nature flowing in one forward direction only as they do not cross the zero axis point. Common uni-directional waveforms include Square-wave timing signals, Clock pulses and Trigger pulses.
- 2. Bi-directional Waveforms: These waveforms are also called alternating waveforms as they alternate from a positive direction to a negative direction constantly crossing the zero axis point as they go through periodic changes in amplitude, with the most common by far being the Sine-wave.
Method II:
Based on periodicity:
- Periodic Waveforms: These waveforms repeat themselves after a specified period of time called the TIME PERIOD, generally denoted as ‘T’.Their nature can be easily predicted at any instant of time.
- Non-Periodic Waveforms: These waveforms don’t repeat themselves after a specified period of time. When compared to periodic waveforms, prediction of their nature is quite difficult.
Method III:
- Sinusoidal Waveforms: Follows sine rule.
- Non - Sinusoidal Waveforms: Doesn't follow sine rule.
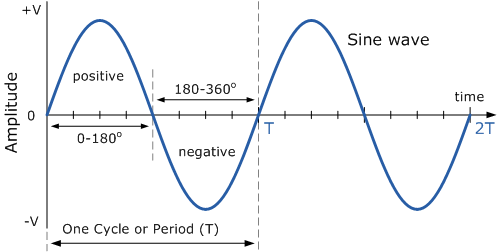
SINE WAVE:
A sine wave is a waveform that follows the sine rule. Even a cosine wave is a form of sine wave shifted by a phase angle of 90 degrees.
The basic parameters required to define a sine waveform are:
MAXIMUM POSITIVE AMPLITUDE (A+):
As the name suggests it is the maximum amplitude above the time axis. It has the unit of which ever quantity is represented on the vertical axis.
MAXIMUM NEGATIVE AMPLITUDE (A-):
As the name suggests it is the maximum amplitude below the time axis. It has the unit of which ever quantity is represented on the vertical axis.
In case of a symmetrical waveform,
(A+) = (A-)
TIME PERIOD (T):
The time period T is the time for one complete cycle of an oscillation of a wave. Its unit is seconds.
FREQUENCY (f):
The frequency ‘f’ is the number of periods per unit time (per second). Its unit is Hertz.
Frequency and Time period are related as:
f = (1/T)
PHASE SHIFT (θ):
It’s the shift in phase at time=0 or at a time=t. It is generally the lead or lag of the waveform under consideration with respect to another standard waveform/reference waveform. Its unit is degrees or radians.
OFFSET (Y):
It is the upshift or downshift of a waveform with respect to a standard/reference waveform. It has the unit of which ever quantity is represented on the vertical axis.
A sine wave has a duty cycle of 50%.
So now we can represent a SINE WAVE as:
y=Asin(ωt+ θ) +Y
where A is the effective amplitude.
SQUARE WAVE:
A square wave is a kind of non-sinusoidal waveform, most typically encountered in electronics and signal processing. An ideal square wave alternates regularly and instantaneously between two levels.
The basic parameters required to define a square waveform are:
MAXIMUM POSITIVE AMPLITUDE (A+)
MAXIMUM NEGATIVE AMPLITUDE (A-)
In case of a symmetrical waveform,
(A+) = (A-)
ON TIME (Ton):
It is the time for which the waveform stays is high state or at a maximum level in one cycle. Its unit is seconds.
OFF TIME (Toff):
It is the time for which the waveform stays is low state or at a minimum level in one cycle. Its unit is seconds.
TIME PERIOD (T):
T=Ton + Toff
FREQUENCY (f)
OFFSET (Y)
DUTY CYCLE (D):
Its is defined as the ratio of on time to the total time period.
D=Ton/T = Ton/(Ton + Toff)
for a symmetrical waveform D=50% or 0.5.
So now we can represent a SQUARE WAVE as:
y = A+ for 0<t<Ton
A- for Ton<t<T
or y = sgn(sin(x))
if (A+)=A then (A-)=(A+) + Y
RECTANGULAR WAVE:
A square wave with D≠50% is called as rectangular waveform.
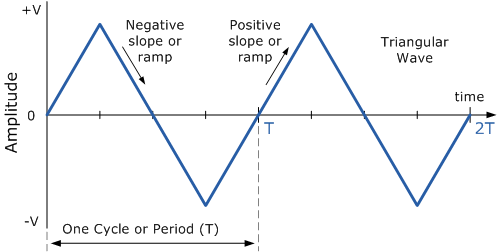
TRIANGULAR WAVEFORM:
Triangular Waveforms are generally bi-directional non-sinusoidal waveforms that oscillate between a positive and a negative peak value. Although called a triangular waveform, the triangular wave is actually more of a symmetrical linear ramp waveform because it is simply a slow rising and falling voltage signal at a constant frequency or rate. The rate at which the voltage changes between each ramp direction is equal during both halves of the cycle.
The basic parameters required to define a triangular waveform are:
MAXIMUM POSITIVE AMPLITUDE (A+)
MAXIMUM NEGATIVE AMPLITUDE (A-)
In case of a symmetrical waveform,
(A+) = (A-)
TIME PERIOD (T)
FREQUENCY (f)
OFFSET (Y)
RISING SLOPE(M+):
It is the slope of the positive ramp.
FALLING SLOPE(M-):
It is the slope of the negative ramp.
For a symmetrical waveform,
(M+) = - (M-)
So now we can represent a TRIANGULAR WAVE as:
y = (M+)t for 0<t<(T/4)
(M-)t for (T/4)<t<(3T/4)
(M+)t for (3T/4)<t<T
or y = ∫sgn(sin(x))dx
SAWTOOTH WAVE:
Sawtooth Waveforms are another type of periodic waveform. As its name suggests, the shape of the waveform resembles the teeth of a saw blade. Sawtooth waveforms can have a mirror image of themselves, by having either a slow-rising but extremely steep decay, or an extremely steep almost vertical rise and a slow-decay.
The basic parameters required to define a sawtooth waveform are:
MAXIMUM POSITIVE AMPLITUDE (A+)
TIME PERIOD (T)
FREQUENCY (f)
OFFSET (Y)
RISING SLOPE(M+):
It is the slope of the positive ramp.
OR
FALLING SLOPE(M-):
It is the slope of the negative ramp.
So now we can represent a SAWTOOTH WAVE as:
y = (M+)t for 0<t<T for Positive Ramp
OR
(M-)t for 0<t<T for Negative Ramp
or y = t – floor(t)
TRIGGERS AND PULSES:
Although technically Triggers and Pulses are two separate waveforms, we can combine them together here, as a "Trigger" is basically a very narrow "Pulse". The difference being a trigger can be positive or negative in direction were as a pulse is only positive in direction. A Pulse Waveform or "Pulse-train" as they are more commonly called, is a type of non-sinusoidal waveform that is similar to the Rectangular waveform we looked at earlier. The difference being that the exact shape of the pulse is determined by the "Mark-to-Space" ratio of the period and for a pulse or trigger waveform the Mark portion of the wave is very short with a rapid rise and decay shape as shown below.PULSE WAVE:
 |
GENERATION OF SINE,SQUARE AND TRIANGULAR WAVEFORMS:
Now comes the interesting part.Lets generate square,sine and triangular waveforms using ICL8038.The circuit is as shown below:
